Теория вероятности: как использовать ее для лучшего принятия решений

Факторы, влияющие на принятие решений

На самом деле объем темы факторов, влияющих на процесс принятия решений, очень велик, поэтому мы осветим только наиболее важные на наш взгляд тонкости, самым прямым образом воздействующие на совершение выбора и его эффективность.

В первую очередь это личностные факторы. К ним относятся психические свойства, состояния и процессы. Далее идут факторы ситуационные: внешние и внутренние. Внешняя среда – это экономические и политические условия, правовые нормы, социокультурные факторы и технологии, природно-географические факторы. Деловая сфера здесь также дополняется потребителями, поставщиками, конкурентами, инфраструктурой – все это имеет значение. Внутренняя среда – это цели и структура организации, корпоративная культура, организационные процессы и имеющиеся ресурсы

Говоря о среде принятия решений, не менее важно упомянуть о рисках, определенности и неопределенности, времени и изменениях самой среды

Есть также и неопределенные факторы (они различаются по источнику неопределенности (неопределенность среды или личная неопределенность), по природе (случайные или неслучайные)), информационные и поведенческие факторы, а также отрицательные последствия и взаимосвязанность решений.

Как вы и сами видите, тема факторов, влияющих на принятие решений, не только очень интересна, но и широка

Чтобы лучше разобраться в ней, а также вообще в том, как люди принимают решения, можно (настоятельно рекомендуется тем, кто хочет стать специалистом в этой области), обратить внимание на теорию принятия решений. Она способна дать ответы на многие вопросы

Литература

• Литвак Б. Г. Разработка управленческого решения — М.: Издательство «Дело», 2004 г. — 392 с.
• Литвак Б. Г. Экспертные оценки и принятие решений.- М.: Патент, 1996. — 271 с.
• Хемди А. Таха Глава 14. Теория игр и принятия решений // Введение в исследование операций = Operations Research: An Introduction. — 7-е изд. — М.: «Вильямс», 2007. — С. 549-594. — ISBN 0-13-032374-8

• Г. Тейл. Экономические прогнозы и принятие решений. М.: «Прогресс» 1970.
• К. Д. Льюис. Методы прогнозирования экономических показателей. М.: «Финансы и статистика» 1986.
• Г. С. Кильдишев, А. А. Френкель. Анализ временных рядов и прогнозирование. М.: «Статистика» 1973.
• Дж.-О. Ким, Ч. У. Мьюллер, У. Р. Клекка и др. Факторный, дискриминантный и кластерный анализ. М.: «Финансы и статистика» 1989.
• Б. Дюран, П. Оделл. Кластерный анализ. М.: «Статистика» 1977.
• Sven Ove Hansson, «Decision Theory: A Brief Introduction», http://www.infra.kth.se/~soh/decisiontheory.pdf (an excellent non-technical and fairly comprehensive primer)
• Paul Goodwin and George Wright, Decision Analysis for Management Judgment, 3rd edition. Chichester: Wiley, 2004 ISBN 0-470-86108-8 (covers both normative and descriptive theory)
• Robert Clemen. Making Hard Decisions: An Introduction to Decision Analysis, 2nd edition. Belmont CA: Duxbury Press, 1996. (covers normative decision theory)
• D.W. North. «A tutorial introduction to decision theory». IEEE Trans. Systems Science and Cybernetics, 4(3), 1968. Reprinted in Shafer & Pearl. (also about normative decision theory)
• Glenn Shafer and Judea Pearl, editors. Readings in uncertain reasoning. Morgan Kaufmann, San Mateo, CA, 1990.
• Howard Raiffa Decision Analysis: Introductory Readings on Choices Under Uncertainty. McGraw Hill. 1997. ISBN 0-07-052579-X
• Morris De Groot Optimal Statistical Decisions. Wiley Classics Library. 2004. (Originally published 1970.) ISBN 0-471-68029-X.
• Khemani , Karan, Ignorance is Bliss: A study on how and why humans depend on recognition heuristics in social relationships, the equity markets and the brand market-place, thereby making successful decisions, 2005.
• J.Q. Smith Decision Analysis: A Bayesian Approach. Chapman and Hall. 1988. ISBN 0-412-27520-1
• Akerlof, George A. and Janet L. YELLEN, Rational Models of Irrational Behavior
• Arthur, W. Brian, Designing Economic Agents that Act like Human Agents: A Behavioral Approach to Bounded Rationality
• James O. Berger Statistical Decision Theory and Bayesian Analysis. Second Edition. 1980. Springer Series in Statistics. ISBN 0-387-96098-8.
• Goode, Erica. (2001) In Weird Math of Choices, 6 Choices Can Beat 600. The New York Times. Retrieved May 16, 2005.
• Anderson, Barry F. The Three Secrets of Wise Decision Making. Single Reef Press. 2002. ISBN 0-9722177-0-3.

Решения на основе суждений

Решения, принятые на основе суждений, могут на первый взгляд показаться интуитивными. Причиной тому – неочевидность логики. Но в действительности такие решения – продукт знаний и накопленного опыта. Люди применяют знания о том, что происходило в подобных случаях в прошлом, для поиска альтернативных выборов в настоящем и прогнозирования их результатов в будущем. Беря за основу здравый смысл, человек принимает решение, успешное ранее. Суждение выступает основой решения, и это полезно, ведь многие жизненные ситуации зачастую повторяются. Поэтому то, что принесло пользу тогда, может принести ее и сейчас.

Учитывая то, что решение на основе суждения принимается в сознании человека, оно всегда будет отличаться быстротой и невысокой «ценой». Однако здравый смысл в чистом виде – явление очень редкое, т.к. у каждого есть свои потребности, задачи, убеждения и т.д. Так что одних суждений для принятия решений маловато в уникальных и сложных ситуациях, где проблемы лишь кажутся очевидными.

Если ситуация новая и у человека еще нет опыта, он не может обосновать свой выбор логически. Суждения здесь могут оказаться плохими, т.к. факторов, которые нужно учитывать, очень много, и разум не способен обработать их все сразу в силу ограниченности своих возможностей. Исходя из того, что суждение берет за основу опыт, слишком большая ориентация на последний может смещать решения в стороны, знакомые человеку по действиям в прошлом. В такой ситуации очень просто не заметить хороших альтернатив. Но еще важнее то, что человек, слишком уповающий на суждения и опыт, может осознанно или неосознанно избегать нового. А это в свою очередь может стать причиной больших проблем в будущем, ведь актуальность практически любой информации со временем снижается.

Адаптироваться к новому и тем более сложному никогда не бывает слишком просто, ведь всегда существует вероятность принятия неверного решения. Но во множестве ситуаций человек вполне может повысить свои шансы на правильный выбор – если только он попробует принять решение рационально.

Общие сведения о правилах принятия решений

При принятии решений, следует руководствоваться соответствующими правилами. На первом этапе – определение цели. Принимающий решение сам выбирает, каким правилом ему воспользоваться, потому что для каждого случая применимо какое-то определенное правило.

Они делятся на две группы:

– правила принятия решений без использования численных значений вероятностей исходов;

– правила принятия решений с использованием численных значений вероятностей исходов.

На практике, поиск наиболее оптимального решения начинается с перечисления возможных вариантов и их предполагаемых исходов. Анализ существующих данных и проведение дополнительных исследований, которые формируют информационную среду, позволяет снизить уровень неопределенности и принимать эффективные решения.

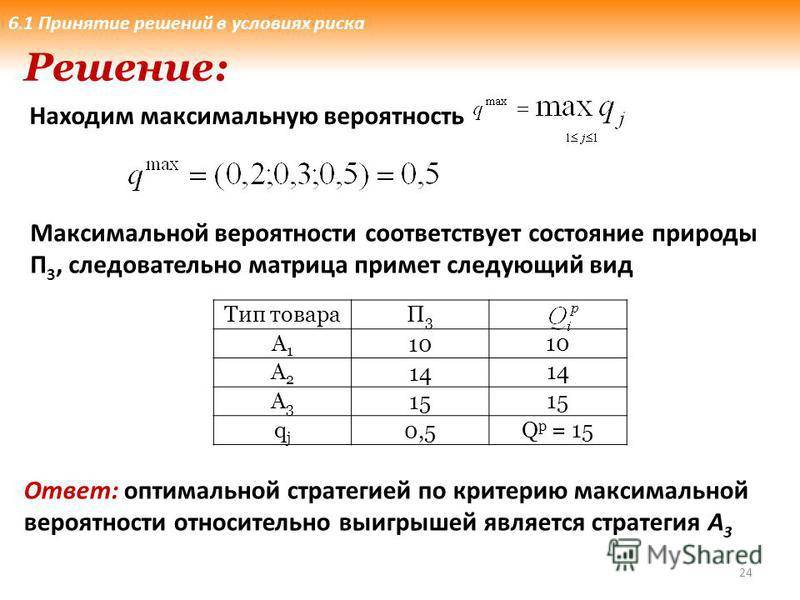
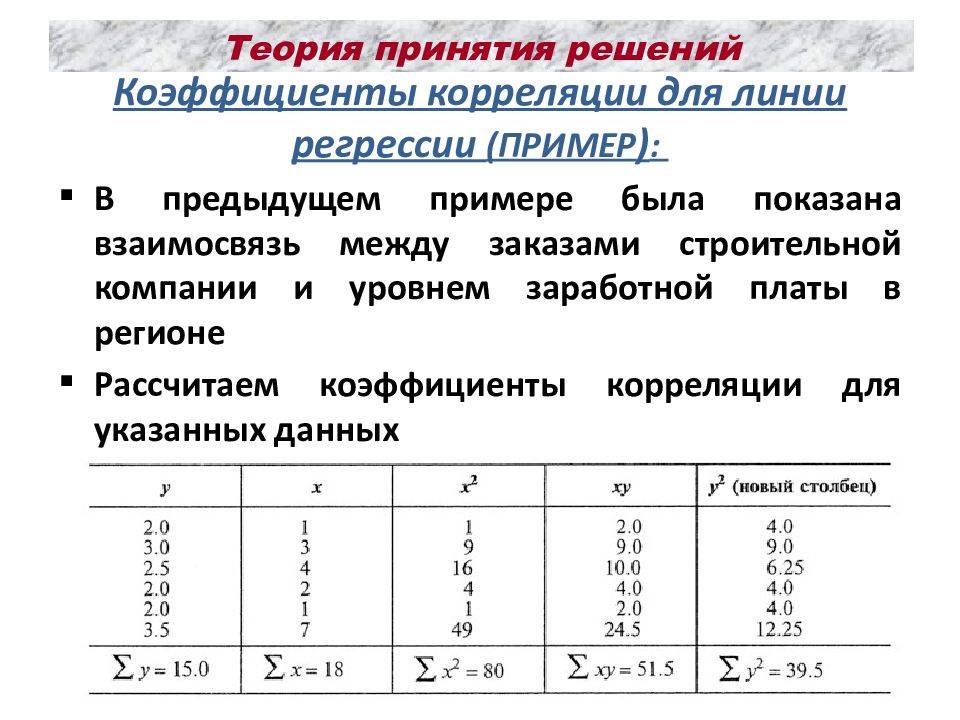
К методам принятия решений, учитывающим вероятности возникновения каждого исхода, относятся “правило максимальной вероятности” и “правило оптимизации математических ожиданий”.

При данных методах составляется таблица доходов, в которой указываются все возможные варианты доходов и вероятности их наступления.

При использовании правила максимальной вероятности соответственно выбирается один из исходов, имеющий максимальную вероятность по правилу максимаксного или минимаксного решения. Вероятность определяется как относительная частота каждого возможного исхода на основании показателей реализации продукции и анализа потребностей покупателей. В случаях, если несколько решений имеют максимальную вероятность, то, используя правило максимакса, оценивается их возможный доход и выбирается наибольший.

При использовании правила оптимизации математических ожиданий высчитываются математические ожидания для доходов или потерь и затем выбирается оптимальный вариант.

На основании исходных данных вероятность каждого исхода и значения из таблицы возможных доходов вычисляется для каждого решения математическое ожидание дохода и далее выбирается максимальное значение.

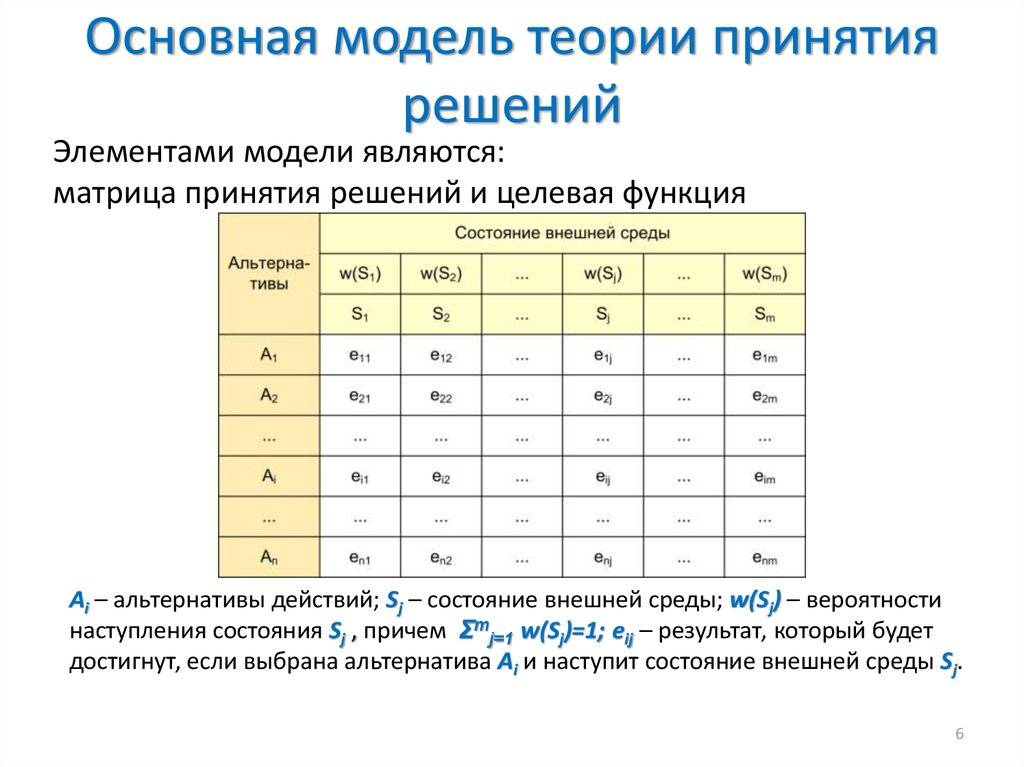
Зачем нужна теория вероятности

Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.

Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.

Альтернативы теории вероятностей[править]

Очень спорная проблема — можно ли заменить использование вероятности в теории решения другими альтернативами. Сторонники нечёткой логики, теории возможностей, теории очевидностей Демпстера-Шафера и др. поддерживают точку зрения, что вероятность — только одна из многих альтернатив, и указывают на многие примеры, где нестандартные альтернативы использовались с явным успехом. Защитники теории вероятностей указывают на:

• работу Ричарда Трелкелда Кокса по оправданию аксиом теории вероятностей;
• парадоксы Бруно де Финетти как иллюстрацию теоретических трудностей, которые могут возникнуть благодаря отказу от аксиом теории вероятностей;
• Теоремы совершенных классов, которые показывают, что все допустимые решающие правила эквивалентны байесовскому решающему правилу с некоторым априорным распределением (возможно, неподходящим) и некоторой функции полезности. Таким образом, для любого решающего правила, порождённого невероятностными методами, либо есть эквивалентное байесовское правило, либо есть байесовское правило, которое никогда не хуже, но (по крайней мере) иногда и лучше.

Действительнозначность вероятностной меры под сомнение была поставлена только однажды — Дж. М. Кейнсом в его трактате «Вероятность» (1910 год). Но сам автор в 30-х годах назвал эту работу «самой худшей и наивной» из его работ. И в 30-х годах стал активным приверженцем аксиоматики Колмогорова — Р. фон Мизеса и никогда не ставил её под сомнение. Конечность вероятности и счётная аддитивность — это сильные ограничения, но попытка убрать их, не разрушив здания всей теории, оказались тщетными. Это в 1974 году признал один из самых ярких критиков аксиоматики Колмогорова — Бруно де Финетти.

Более того, он показал фактически обратное — отказ от счётной аддитивности делает невозможными операции интегрирования и дифференцирования и, следовательно, не даёт возможности использовать аппарат математического анализа в теории вероятностей. Поэтому задача отказа от счетной аддитивности — это не задача реформирования теории вероятностей, это задача отказа от использования методов математического анализа при исследовании реального мира.

Попытки же отказаться от конечности вероятностей привели к построению теории вероятностей с несколькими вероятностными пространствами, на каждом из которых выполнялись аксиомы Колмогорова, но суммарно вероятность уже не должна была быть конечной. Но пока неизвестно каких-либо содержательных результатов, которые могли бы быть получены в рамках этой аксиоматики, но не в рамках аксиоматики Колмогорова. Поэтому это обобщение аксиом Колмогорова пока носит чисто схоластический характер.

С. Гафуров полагает, что принципиальным отличием теории вероятности Кейнса (а, следовательно, и математической статистики) от колмогоровской (Фон Мизеса и пр.) является то, что Кейнс рассматривает статистику с точки зрения теории принятия решений для нестационарных рядов. Для Колмогорова, Фон Мизеса, Фишера и пр. статистика и вероятность применяются для существенно стационарных и эргодичных (при правильно подобранных данных) рядов — окружающего нас физического мира.

Известно, что теория нечётких множеств (англ. fuzzy sets) в определённом смысле сводится к теории случайных множеств, то есть к теории вероятностей. Соответствующий цикл теорем приведён в книгах А. И. Орлова, в том числе указанных в списке литературы ниже.

Условная вероятность

Иногда можно перемножать вероятности событий, не являющихся в полном смысле слова независимыми. Пусть для того, чтобы произошло событие А, необходимо, чтобы последовательно произошли В и С. В зависимости от того, произошло ли В, вероятность С может отличаться. Например, в урне лежат 4 шарика – 2 красных и 2 желтых. Предположим, что произошло событие В – был вытащен красный шар. Его вероятность равна 0,5. Чему тогда равна вероятность события С – вытаскивания желтого шарика? В урне осталось 3 шара, из них 2 желтых, поэтому Р(С) = 2/3.

С другой стороны, пусть В не произошло, то есть первым был вынут желтый шар. Чему тогда равна вероятность С? В урне снова 3 шарика, но лишь 1 из них желтый. Следовательно, Р(С) = 1/3. Получается, что в зависимости от того, случилось ли В, вероятность Р(С) принимает разные значения. В математике такую вероятность называют условной.

Обозначается она так:

Р(С|B).

Первая буква в скобках соответствует событию, для которого указываем вероятность, а вторая буква – событию, которое является условием для С.

Если событие А произойдет тогда, когда свершится сначала В, а потом С, то вероятность А также можно найти с помощью умножения

Р(А) = Р(В)•Р(С|B)

Пример. В урне находится 52 шара, из них на 4 написана буква Т. Из урны последовательно вынимаются два шара. Какова вероятность, что на обоих вытащенных шарах будет буква Т?

Решение. Так как в урне 52 шара, и лишь на 4 есть буква Т, то шанс на то, что первым вытащат именно шар с буквой Т, равен 4/52 = 1/13. Если это событие произошло, то в урне остался 51 шар, и лишь на трех будет находиться нужный символ. Тогда вероятность появления шара с буквой Т составит 3/51 = 1/17. Общая же вероятность появления 2 таких шаров подряд найдется как произведение этих вероятностей:

Р = (1/13)•(1/17) = 1/221 ≈ 0,004525

Эту вероятность можно рассчитать и иначе, по аналогии с задачей про бракованные велосипеды, которая приведена выше. Подсчитаем, сколькими способами можно выбрать 2 шара из 52:

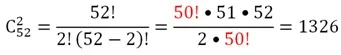
Но всего 6 способами можно выбрать 2 шара из 4:

Поделив число благоприятных исходов на их общее количество, получим искомую вероятность:

Р = 6/1326 = 1/221.

Ответ: 1/221

Пример. Известно, что вероятность мужчины дожить до 90 лет составляет 5,126%, а до 95 лет – 1,326%. С какой вероятностью мужчина, которому уже сейчас 90 лет, доживет до 95 лет?

Решение. Пусть А – это дожитие до 95 лет, С – дожитие 90-летнего мужчины до 95 лет, В – дожитие до 90 лет. Чтобы отпраздновать 95-летие, человек сначала должен отметить 90-летний юбилей, а потом ещё прожить 5 лет. Другими словами, чтобы случилось А, сначала должно случиться В, а потом событие С при условии В. То есть можно записать

Р(А) = Р(В)•Р(С|B)

По условию Р(А) = 0,01326, а Р(В) = 0,05126. Зная это, легко найдем Р(С|B):

Р(А) = Р(В)•Р(С|B)

0,01326 = 0,05126•Р(С|B)

Р(С|B) = 0,01326/0,05126 ≈ 0,2587

Это и есть вероятность мужчины, отметившего 90-ый день рождения, дожить до 95 лет.

Ответ: 0,2587

Парадокс выбора

Наблюдаемый во многих случаях парадокс, когда больший выбор может привести к более бедному решению или, вообще, к отказу принять решение. Иногда это теоретически объясняется тем, что называется «параличом анализа», реального или воспринятого, а также, возможно, «рациональным невежеством». Много исследователей, включая Шину С. Ииенгара и Марка Р. Леппера (Sheena S. Iyengar and Mark R. Lepper), опубликовало исследования этого явления. (Goode, 2001)

Так же, у нас сейчас есть центральная проблема выбора – свобода выбора. В понимании Барри Швортца выбор не сделал нас свободнее, но ограничил, не сделал нас счастливее, но постоянно вызывает неудовлетворенность

Закономерности

Я подкинул монету 10 раз. В результате, орел выпал 7 раз, а решка выпала 3 раза. Получилась разница 7 – 3 = 4.

Я подкинул монету 100 раз. В результате, орел выпал 56 раз, а решка выпала 54 раза. Разница получилась еще больше 56 – 44 = 12.

Я подкинул монету 1000 раз. Теперь, наоборот, орлов выпало меньше, всего 485 раз. А решек выпало 515 раз. Разница стала еще больше, но со знаком минус, так как орлов теперь меньше: 485 – 515 = -30.

Где же закономерность?

Закономерность в том, что при увеличении числа подбрасываний монеты примерно в половине случаев выпадает орел, а в половине решка, и при этом относительное отклонение от половины стремится к нулю с
увеличением числа испытаний. Проверим это.

• 10 подбрасываний. 10:2=5. Абсолютные отклонения от 5: орлы 7-5=+2, решки 3-5=-2. Относительные отклонения от 5: орлы +2/5=+0.4, решки -2/5=-0.4.
• 100 подбрасываний. 100:2=50. Абсолютные отклонения от 50: орлы 56-50=+6, решки 44-50=-6. Относительные отклонения от 50: орлы +6/50=+0.12, решки -6/50=-0.12.
• 1000 подбрасываний. 1000:2=500. Абсолютные отклонения от 500: орлы 485-500=-15, решки 515-500=+15. Относительные отклонения от 500: орлы -15/500=-0.03, решки +15/500=+0.03.

Таким образом, относительное отклонение от половины резко уменьшается с ростом числа испытаний.

• 10 подбрасываний. Отклонение 40%.
• 100 подбрасываний. Отклонение 12%.
• 1000 подбрасываний. Отклонение 3%.

Вы можете провести свои испытания, и Вас получатся другие цифры. Но тенденция будет такая же.

Еще одна закономерность будет проявляться в том, что отклонений в пользу большего числа решек будет столько же, сколько отклонений в пользу большего числа орлов. Например, если проводить серию по 10
испытаний, то у меня получилось в первой серии, что орлов больше, чем решек. Но когда я провел 10 таких серий по 10 испытаний, то орлов было больше в семи сериях из 10 серий.

Затем я провел 100 серий по 10 бросаний в каждой. Теперь решек было больше в 55 серий, а орлов было больше в 45 сериях. Хотя по абсолютной величине не получается, чтобы в 50% всех серий было больше
отклонений в пользу решек, а в 50% всех серий в пользу орлов, но, тем не менее, относительная разница стремиться к нулю при увеличении числа серий испытаний.

Третья закономерность, это симметрия в отклонениях в пользу решек и в пользу орлов. Если делать много серий испытаний с одинаковыми длинами этих серий, то примерно сколько раз было больше в серии
орлов, столько же раз было больше и решек. И чем большее число серий сделать, тем относительная разница между большим выпадением орлов и большим выпадением решек будет стремиться к нулю.

Четвертая закономерность, это распределение отклонений от теоретического. Если провести большое число серий одинаковой длины с подбрасыванием монеты, то можно увидеть, что больше всего будет таких серий,
где отклонений от 50% не будет. Поменьше будет таких серий, где отклонений от 50% будет всего на единицу. Еще меньше будет серий, где отклонений от 50% будет на 2. И так далее. Чем больше отклонение от
теоретического выпадения 50% решек и 50% орлов, тем реже встречается серия подбрасываний с таким отклонением.

Относительная частота случайного события, это отношение количества случаев появления этого события M к общему числу проведенных испытаний N.

Эксперименты показывают, что при многократном повторении испытаний относительная частота M/N случайного события обладает некоторой устойчивостью. Эта устойчивость относительной частоты объясняется
существованием объективных свойств и закономерностей случайного события.

Частота и вероятность

В мире происходят события, которые можно предсказать. Например, можно предсказать приезд лифта после того, как человек нажмет кнопку его вызова. Астрономы могут заранее предсказывать солнечные и лунные затмения.

Однако нередко нам приходится иметь дело с событиями, результат которых заранее предсказать невозможно. Не получается заранее сказать, упадет ли монетка при подбрасывании орлом вверх, также как нельзя заранее предсказать поломку прибора. Такие события называются случайными.

Случайные события обычно могут произойти только в определенной ситуации. Так, событие «выпадение решки» может произойти только при броске монеты. В математике подбрасывание монетки будет называться испытанием или экспериментом.

Здесь не следует воспринимать термин «эксперимент» как некое научное исследование. Испытанием может оказаться любая жизненная ситуация. Приведем несколько примеров опытов и соответствующих им случайных событий:

• Бросок кубика с 6 гранями – это эксперимент, а выпадение или невыпадение шестерки на нем – это случайное событие.
• Полет самолета – испытание, а отказ двигателя в полете – это случайное событие.
• Ожидание автобуса на остановке в течение 10 минут – эксперимент, а появление или непоявление автобуса в этот промежуток времени – случайное событие.
• Футбольный матч – опыт, а победа в нем команды хозяев или травма одного из игроков – случайное событие.
• Выстрел из винтовки – испытание, а попадание в мишень – случайное событие.
• Изготовление рабочим детали – эксперимент, а получение бракованной детали – случайное событие.

Здесь важно отметить, что для математики не важно, является ли событие по-настоящему случайным. Возможно, что автобус ходит строго по расписанию, и человек, знающий его, точно может определить, через сколько минут он приедет

Но если рядом стоит другой человек, не знающий этой информации, то для него приезд автобуса будет случайным событием.

Предположим, что есть возможность провести какой-то эксперимент множество раз. Например, кубик можно бросить 500 раз. Обозначим это число, количество экспериментов, как n. В ходе серии этих бросков шестерка выпала, например, 85 раз. Обозначим эту величину, количество произошедших случайных событий, как m. Само событие «выпадение шестерки» обозначим как А. Тогда отношение m/n будет называться частотой случайного события А. В данном случае частота события А равна

85/500 = 0,17

Наблюдения показывают, что если условия экспериментов примерно одинаковы, а их число велико, то частота одного и того же события будет примерно одинаковой. Чем больше число испытаний, тем обычно ближе частота события к некоторому постоянному числу. Это число и называют вероятностью случайного события А.

Грубо говоря, частота и вероятность событий – это примерно одно и то же. Частоту определяют на практике, входе эксперимента, а вероятность можно рассчитать аналитически.

Вероятность – это величина, которая характеризует возможность события произойти. Если она близка к единице, то событие, скорее всего, произойдет. Если она близка к нулю, то событие, скорее всего, не случится. Для обозначения вероятности используется буква Р. Если надо указать вероятность конкретного события А, то его записывают как Р(А).

Вероятность – это безразмерная величина, то есть для нее нет никакой единицы измерения. Она может принимать значение от 0 до 1. Иногда на практике ее указывают в . Например, вероятность 0,5 означает 50%. Чтобы перевести вероятность в проценты, ее надо просто умножить на 100.

Как решать задачи на вероятность

Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Но как решать задачи на вероятность. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Таким образом подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов. Например, шанс получить решку при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.

Как мы уже с вами увидели, вероятность может быть выражена как в процентах, так и в обычных числах

Важно: на ЕГЭ вам нужно будет записать ответ в числах, не в процентах. Принято, что вероятность изменяется от 0 (никогда не произойдет) до 1 (абсолютно точно произойдет)

Также можно сказать, что всегда

Вероятность подходящих событий + вероятность неподходящих событий = 1

Теперь мы точно понимаем, как считать вероятность отдельного события, и даже такие задачи есть в банке ФИПИ, но понятно, что на этом всё не заканчивается. Чтобы жизнь была веселее, в задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.

Ошибки первого и второго рода[править]

Разделение ошибочных решений на ошибки первого и второго рода вызвано тем, что последствия от разного рода ошибочных решений принципиально различаются в части того, что упущенный выигрыш оказывает меньшее влияние на ситуацию, чем реализованный проигрыш. Например, для биржевого трейдера последствия того, что акции не были куплены, когда их следовало покупать, отличаются от последствий ситуации, когда акции были куплены, но покупать их не следовало. Первая ситуация может означать упущенную выгоду, вторая — прямые потери вплоть до разорения трейдера. Аналогично для политика отказ от захвата власти в революционной ситуации отличается по последствиям от проигранной попытки захватить власть. Для генерала начать военную операцию, которая будет проиграна, гораздо хуже, чем упустить ситуацию, когда можно было провести успешную операцию.
Вместе с тем, классификация ошибок первого и второго рода допустима только в ситуациях, когда ведется точный учёт и анализ рисков. Так, С. Гафуров отмечал для ситуации биржевых брокеров: «Многие полагают, что стратегическая задача аналитических служб (в отличие от прочих подразделений инвестиционных компаний) — не увеличение прибыли, а минимизация возможных потерь. И это принципиальное отличие. С точки зрения теории игр оптимальные решения аналитиков должны отличаться от оптимальных трейдерских действий. Предполагается, что оптимальные стратегии, реализованные в рекомендациях аналитиков, исходят из принципа минимизации максимальных проигрышей (минимакса), в то время как для трейдеров минимакс — неприемлемая стратегия (минимизация максимального проигрыша на рынке — не играть), и в общем виде оптимизация решений трейдеров формализуется только с точки зрения байесовского подхода. Отсюда и необходимость специальных функциональных подразделений, обеспечивающих баланс стратегий, — управляющих фондами. Компании ожидают от фондовых аналитиков непредвзятых прогнозов и обоснованных рекомендаций. Одни свойства таких прогнозов очевидны: точность, достоверность. Другие, такие как воспроизводимость, методологическая корректность или робастность (независимость результатов прогноза от системы координат), часто остаются вне поля зрения как специалистов, делающих прогнозы, так и тех, кто эти прогнозы оценивает».

Вероятность и случайная величина

Вероятность, это количественная мера наступления какого-нибудь случайного события.

Вероятность является первичным базовым понятием в математике, и ее нельзя определить через более простые термины и понятия.

Случайная величина, это такая величина, которая принимает те или иные значения с определенными вероятностями.

Вероятность может принимать значение от нуля до единицы (0⩽P⩽1). Ноль означает невозможное событие (P=0). Единица означает достоверное событие, которое обязательно случится
(P=1).

Например, Вы держите в руке тяжелую гирю и выпускаете её из рук. С вероятностью P=1 гиря упадет вниз. С вероятностью P=0 гиря зависнет в воздухе как в невесомости.

Еще пример. Вы подбрасываете 6-гранный кубик с пронумерованными гранями. Два очка выпадет с вероятностью P=1/6, то есть примерно в каждом шестом испытании. Пять очков тоже выпадет с вероятностью
P=1/6, то есть тоже в каждом шестом испытании.

А теперь более хитрый пример. Вы подбрасываете монету. Вероятность выпадения решки равна вероятности выпадения орла. И та и другая вероятность равна половине (P=1/2).

А может ли монета после подбрасывания встать вертикально на ребро? В прошлом примере мы считали, что это невозможное событие, то есть вероятность такого события P=0. Однако, теоретически такое
случайное событие может произойти. Но вероятность такого случайного события очень-очень маленькая. Возможно, более вероятно, что Вам на голову когда-нибудь упадет метеорит, чем Вы увидите, как после
подбрасывания, монета встала на своё ребро.

Пусть вероятность того, что монета встанет на своё ребро будет P=0.0000002. (Это на самом деле не так, это число взято только для примера.) Чему тогда равна вероятность выпадения орла?

Эта вероятность уже не будет равной P=0.5, так как сумма вероятности всех возможных событий не может быть равной чему-то больше единицы. В самом деле, если мы подбрасываем монету, то или выпадет
решка или выпадет орел или она встанет на ребро. Ничего другого не случится. Значит, вероятность выпадения решки или орла или ребра будет равна единице (P=1). Достоверно произойдет одно из трех
событий.

Поэтому, в силу симметрии между решкой и орлом, получаем, что вероятность выпадения орла будет P=0.4999999. И такая же будет вероятность выпадения решки.

0.4999999 + 0.4999999 + 0.0000002 = 1.

А если монета не может становиться на ребро, то

0.5 + 0.5 = 1.

Для 6-гранного кубика вероятность выпадения каждой из его граней P=1/6. Значит, вероятность того, что выпадет хотя бы одна грань (а это достоверное событие, которое обязательно произойдет) будет

1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.

Теоремы сложения и умножения вероятностей, формулы

Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае .

Последние 2 утверждения называются теоремами сложения и умножения вероятностей.

Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.

Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается «шесть факториал».

В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов В нашем случае .

Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .

В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам

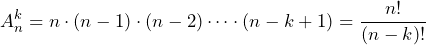
В нашем случае .

И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из элементов по элементам:

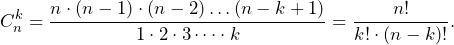
В нашем случае .